
 |
|
|
#1 (permalink) |
|
Location: Waterloo, Ontario
|
How to solve ShapeShifter...
I'm dating a girl who likes to play on Neopets (what can I say, I like'em young!), where you can get neopoints (in-game currency) by succeeding in various games. One such game is Shapeshifter. It looks like this:
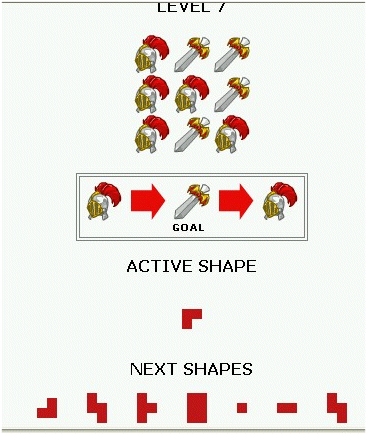 The object of the game is to place the various shapes, in order, on the board, so that all the symbols are the goal symbol, as indicated in the diagram with the big red arrows. Each symbol that's under a shape placed on the board gets turned into the next symbol according to, again, the big red arrow diagram. I think it's fairly self explanatory. My question is how can one solve this puzzle, efficiently? It started out as a simple software project that I did for the fun of it, since the puzzle seemed so interesting to me and it's rated as "extremely difficult" by Neopets. My first implementation simply recursed through all possible board positions to find a solution. This worked for a while but, as you solved one puzzle after the other, they gradually become much harder and, subsequently, the program had to run much longer. Eventually, I added a progress bar and a prediction as to when the program will solve the puzzle, since no one likes to wait around without knowing how much longer you'll things will take. In actuality, the program can't really know how long it will take but it could calculate an upper bound for the time needed and that's what it reported. Much to my chagrin, it didn't take long before the upper bound time to solution was measured in years! So, not one to easily give up, I was forced to actually think about the problem. What will follow is a description of the evolution of my current implementation for solving Shapeshifter. If you'd rather not be told of any of the properties of the puzzle so that you can solve it "entirely by yourself," then don't look into the spoiler tags. Spoiler: I brought it up with some friends and one of them, Yakk actually (and why to links penetrate the spoiler tag?), pointed out that the corners could only be reached in one way, and sometimes not even at all! While it was not immediately obvious how this fact can be used to my advantage, it was clearly a restriction of the solution space and, thus, (theoretically) something that can shorten my search time. After mulling over the problem for a while, other properties of the puzzle occured to me. The order that the shapes are applied is irrelevant. The special properties of the corners can be generalized to all the points on the board. Not every shape can reach every piece. Each board point has certain shapes that can reach it and in a varying number of ways. Finally, each piece needs a specific number number of pieces to solve it. In the case of two symbols (such as the puzzle image used here) a board point that's already the target symbol needs an even number of shapes on it, while another point that's not the target symbol needs an odd number of them. After these considerations, I concieved of a different algorithm. Inspect the puzzle one board point at a time. Sort them in order of available shape positions on them. For each board point to inspect, iterate over all possible combinations of necessary numbers of shapes that will solve that board point and recurse. Surprisingly, this drastically reduces the number of board positions being evaluated and cuts tree searches off earlier. This reduces time to solutions to within a day, rather than years! Now that's an optimisation! Still, a day is a rather long time to wait for a solution. Can't we do better? With a few refinements and some micro-optimisations, I've been able to reduce time to solution to (experimentally, since execution times with algorithms this complex are too hard to calculate accurately) within two or so hours. Not bad but still... Can we still do better? So, here I am. I'm almost at my end. There's one last property of the puzzle that I was able discern recently and, thus, one last optimisation I can make but it won't recduce hours to seconds. Spoiler: If you look at the sheer number of shapes (it gets worse later on), you can see that there are a fair number of shapes on each square. Counting shape squares and dividing by the number of board points, you will see that the number of shapes over each square can average between 2.4 to 3.7 shapes! Seems a little weird to start guessing number of shapes over a (two symbol) square at zero or one, right? Now, the situation is a little more complicated than that because, since the corners and edges are less accessible, the average number of shapes over a board point varies even within the same puzzle board! Luckily, this just makes the situation more advantagous, not less. The corners average about none, while the center squares can have as many as eight shapes over them! That makes it totally ridiculous to start guessing at zero... while at the corners, you'd want to guess the exact number of shapes needed. But that's it. That's where I am and I'm all out of ideas. If anyone else can think of more that can be done, or if there's a totally foreign appraoch that might do better, please mention it! Thank you... |
|
|
|
|
#5 (permalink) |
|
On the lam
Location: northern va
|
Ok, assuming that you have to use all shapes, here's an extra optimization, related to something else we talked about before: if you color the board as a checkerboard, above you have, say, 5 black and 4 white squares. The number of blocks on black squares has to be 4+2n, while the number of blocks on white squares has to be 1+2n. (As a shortcut, it's probably easier just to say the mod 2 of the number of blocks on black squares is 0, and the mod 2 on the white squares is 1). Now we can assign a pair of numbers for each shape that will be used, depending on the number of white/black squares needed to cover it (order is arbitrary). So for the example above, we have:
2,1 2,1 2,2 3,1 3,3 1,0 1,1 2,2 All of these ordered pairs can be flipped, but the X column has to add up such that the mod 2 of the number is 0, while the sum of the Y column has to have a mod 2 of 1. Does that reduce any time?
__________________
oh baby oh baby, i like gravy. Last edited by rsl12; 11-23-2005 at 10:07 AM.. |
|
|
|
|
#6 (permalink) |
|
On the lam
Location: northern va
|
You'll notice that the number of possiblities is actually pretty small: I'm counting 2*3=6 possibilities in the example above for ways of flipping the ordered pairs (symmetrical pairs need no flipping).
__________________
oh baby oh baby, i like gravy. |
|
|
|
|
#7 (permalink) |
|
On the lam
Location: northern va
|
PS. if the pieces don't rotate, you can try a multi-color scheme. Here's a 3-color scheme:
ABC CAB BCA Each shape then gets a three values associated with it: 1,1,1 1,1,1 2,0,2 2,1,1 2,2,2 1,0,0 1,1,0 2,0,2 In this case the constraints are X mod 2 = 1, Y mod 2 = 1, and Z mod 2 = 1 (you need only check 2 of the 3 however). You can convince yourself that you can 'flip' (or rather, 'rotate') the numbers in any of 3 possible combinations. If you had something that was 1,2,3 you could rotate the values (not the shape) so that it was 2,3,1 3,1,2 but flipping two numbers doesn't work: 1,3,2 would be a different shape (or you would have rotated the shape). In choosing a color scheme, the trick seems to be to get as few numbers that give you the same result when you mod them. [For example, (2,0,4) mod 2 is (0,0,0), and (1,1,1) mod 2 is (1,1,1). You aren't optimizing anything associated with these two guys.] The 3-color scheme, in this case, seems to give you no benefit over the 2-color one (though I could be wrong).
__________________
oh baby oh baby, i like gravy. Last edited by rsl12; 11-23-2005 at 11:03 AM.. |
|
|
|
|
#9 (permalink) | |||
|
Location: Waterloo, Ontario
|
While I appreciate the enthusiasm, you might need to cut back on that coffee...
Quote:
Quote:
Quote:
I'll give your other suggestions some thought... |
|||
|
|
|
|
#10 (permalink) |
|
Insane
|
One added complication, you can place items off board!
So if you have a bar (1,1,1) flip values it can be placed on a board (a.b.c) as (1,1,1),(0,1,1) or (0,0,1)... Edit: Only with some pieces, I don't understand, some pieces can be placed off board other generate an error saying they are off board ! Last edited by AngelicVampire; 11-24-2005 at 01:48 PM.. |
|
|
|
|
#11 (permalink) |
|
Upright
|
Ok, i understand certain things but then there are some items that i don't quite get such as:
~1)<you will see that the number of shapes over each square can average between 2.4 to 3.7 shapes> How were these numbers calculated, because in the above drawing the stapes can fit over almost all pieces with only the corners and some edges as exceptions? Also could you please post some Pseudo-code, so that it is clearer?- For some reason Pseudo-code makes more sense to me, except i don't program, but its still and interesting problem- That i would like to understand better.- If you can it would be greatly appeaciated(sp?) Last edited by Dmner; 12-06-2005 at 07:05 PM.. |
|
|
|
|
#12 (permalink) |
|
Upright
|
Optimized shapeshifting
Hi together,
well, you may improve the algorythem further and solve such puzzeles with up to 64x64 (or 128x128 if your comp supports a 128 bit unit , like AltiVec, etc.) field size in a few minutes. Your one-field approach was a good idea but why not checking against a whole line? Beginning with the last line and as few shapes as possible... To do this FAST you need to convert the field and the shapes into liniar binary data. Your field (from the picture) will become: 100110101 - where 1 needs a odd number of convertions and 0 and even number (or null). Pos 1 is left like: pos 1 was x=0,y=0, pos 2 was x=1,y=0, etc. Now the shapes: Shape 1: 11010 Shape 2: 01011 Shape 3: 01011001 and so on... You need to fill in Zeros up to the X field size. E.g. shape 1 has a width of 2, the field X size is 3, so you need to add 1 Zero to each line, except the last line. You still need to keep possible positions for each shape but this time you need it as offset for the field data - just a single byte per pos. Now you can simply use bit operators to check against the field and other shapes by using XOR and positioning the sahpes by shifting the bits. To keep things simple, starting checking against the last line, solve it and move up line by line. In your example the last line is only 3 bits: 101 As you can see field 1 and 3 of the line needs to be transformed, now find the right shapes - try with as few as possible... If you have a puzzle with 3 or more items, convert them the same way and check for a correct tranformation only if a solution matches the bit field... This way you can compare around 20 mil. positions of 20 shapes per second as long as the field width is less than 64 blocks (or 128). Another improvement would be to find shape combinations that wipe out each other to reduce the number of shapes...but you may end up with no solution this way...However, it worked for me for most tests. Hope that's fast enough  Cheers, Twilight |
|
|
|
|
#13 (permalink) | |
|
Location: Waterloo, Ontario
|
Quote:
Unfortunately, it isn't fast enough... It may sound like a good optimisation but the reality is that these small implementation "tweaks" only improve the runtime by a constant amount. I don't need the program to be twice or four times as fast... Making the program 10,000 times faster may not be fast enough. The problem is that the puzzle grows remarkably fast! The picture in the first post is only the very first level of complexity. The posted algorithm can handle up to 7x8 boards with 18 shapes within a reasonable time (sometimes a couple of hours!). No doubt, the puzzle gets even bigger... So, if you have any suggestions for a faster algorithm rather than implementations of faster routines, I'm keen to hear them! Thanks... |
|
|
|
|
|
#15 (permalink) |
|
Upright
|
Hmm, maybe you have overseen one aspekt of my last post - the row by row thing. This highly reduces the number of possible tries and solutions for the remaining lines.
Usually the last row requires the fewest number of shapes to solve than any other row. Once a row is solved, try to solve the next row with the remaining shapes. Let's take a 8x8 blocks field with 20 shapes. Beginning with the last row, even if the last line requires 14 shapes to be solved, you only have to check, possible shape postions (you only need to multiply all possible x-positions of each shape),e.g.: 2 x 4 x 4 x 8 x 2 x 3 x 4 x 5 x 8 x 3 x 5 x 4 x 6 x 3 = 265.420.800 Why only 14? Easy the 6 remaining shapes are not enough to cover all remaining fields that need to be turned (this may be an additional check in your routine). I guess, you can imagine that is it very unlikely that you need 14 images to solve the last row. In practice you need around numOfShapes/4, with our 20, this would mean 5 shapes to solve the last line... With each solved row you GREATLY reduce further calculations, because both, field size and number of shapes to be tested against are reduced. Just think about it another second... The bit-mask is in fact only a bonus. I've written a small c-prog for that, it checks around 100mil pos/sec. |
|
|
|
|
#16 (permalink) |
|
Lover - Protector - Teacher
Location: Seattle, WA
|
Because each state requires 0 or 1 hits in order to achieve the correct state (the sword thing, in this case), the shapes themselves can be abstracted away and you basically have a "Travelling Salesman" situation, do you not?
If so, your problem is NP-Complete, and intractable. If you solve it, you'd be eligible for almost $7 million in research rewards for solving NP-Complete problems of this type.
__________________
"I'm typing on a computer of science, which is being sent by science wires to a little science server where you can access it. I'm not typing on a computer of philosophy or religion or whatever other thing you think can be used to understand the universe because they're a poor substitute in the role of understanding the universe which exists independent from ourselves." - Willravel |
|
|
|
|
#17 (permalink) | |||
|
Location: Waterloo, Ontario
|
Quote:
By the way, I'm glad to see you participating in various forums, here. Welcome to TFP! Now, to give some more context to the discussion, here's the puzzle that my algorithm finds intractable.  Quote:
I'm guessing that you made all those numbers up just as an example but I don't know why you think that "6 remaining shapes are not enough to cover all remaining fields." Also, I don't know why you think that "the last row requires the fewest number of shapes to solve than any other row." As far as I can tell, how many shapes each row needs to be solved with is independent of each other. Now, I do understand that the edge rows will statistically have fewer shapes on them but this is just as true for the first row as it is for the last. The second row as much as the second last row, etc... This doesn't sound like what you're trying to say. Furthermore, it sounds like you think that after we "solve" one row, we can use that solution to solve the other rows. Again, as far as I can tell, there are multiple solutions for each row and the only way to know which one contributes to the final solution is to iterate over all combinations of them and see which one actually works. Going back to your original post, I'm not sure what distinction you're making between solving "one-field" at a time and "checking against a whole line." In order to check that a line is solved you need to verify that each "field" in the line is solved, right? Finally, is your first language English? If it's not, I'm sure you're doing the best you can and, in all fairness, it's pretty good. If it is your first language, can you proof read your posts, please? Normally, it's not a big deal but when talking about complicated and very technical subjects, grammatical mistakes can seriously impedge clarity. Thank you... As an aside, I can't help but notice that the two posts that you've made in this thread are the only posts you've ever made on this forum. Did you join this forum just to participate in this thread? If so, I find that very interesting. How did you come across it? Quote:
I'm glad people are still reading this thread, especially considering how dead Tilted Knowledge has become. I hope no one has given up and this problem because I haven't quite yet. I actually have some new ideas that I haven't implemented yet. I know they will reduce the execution time, I just don't know if they will reduce it enough and I can't until I actually implement them and run the program. Big bucks, no whammies! Thank you all for participating... |
|||
|
|
|
|
#18 (permalink) |
|
Upright
|
Does the puzzle usually include repeated shapes on the higher difficulties, because if they do, you might be able to reduce the time needed to find a solution by removing a pair and the running the algorithm(s) to see if the puzzle can be solved and just place the repeated shapes on top of eachother. In your example, it could reduce the possibilites to a twelve-thousanth of the number of possibilities you would get if you ran your original algorithm. Though I suppose that would only be for a special case.
|
|
|
|
|
#19 (permalink) | |
|
Location: Waterloo, Ontario
|
Quote:
However, you'll notice that, in the puzzle, there are three states and not just two. So, you would need three similar shapes for your suggestion to make sense. Furthermore, if you think about the likely implementation of the puzzle generator, you'll see that it's exceedingly unlikely that the similar shapes are placed over each other in the final solution... |
|
|
|
|
|
#20 (permalink) |
|
Upright
|
Im not sure to have understood everything written in this post and i might just say a solution that was posted before but ill still give it a try...
On a 6x6 board, a shape is average 3x3 and there's 15 shapes (supposition). That means there is 16 possibilities for each. Now if the solver can make 10k tries (with backtracking)/second, that would take 20828286 years. Inspired by rsl12's post (checkerboard with black = x mod 2 = 0... ), i though that first, the program make 1 try, only one. Then, since every shape has 16 positions but they are grouped in 2 sections : those that activate X black checker and and Y white ones and those that activate Z black checker and and T white ones. Of course, it dosent work with shapes containing a pair number of squares. But still, its not 15^16 anymore but 15^12, giving 411 years instead. Thats a 50677x improvement! But then, if we consider a 4 color scheme, only 1/4 can be divided by 4 (thereforth unaffected) and the numbers of positions availible because divided by 4 instead 2. So it becomes 15^6,75, giving (only...) 2h45! Yeah i know its still alot but thats still infinitly faster then backtracking only. Just for the sake of a number, with a 8 color scheme it would take 15^3,75, giving a mere...3 seconds. My intuition tells me i made a mistake somewhere on how to calculate the amount of time taken, but if im not mistaken you puzzle there should take no more then 1/2 day. If that isn't fast enough just add more color schemes (a good number is Roundup((row+colum)/2*1,25). And if your computer can do more then 10000 tries/second... However, im not a very experimented coder and visual basic isn't the fastest thing ever so i didn't manage to succeed doing this code...  |
|
|
|
|
#21 (permalink) |
|
Upright
|
i was admiring this thread although i do not have any knowledge as to how to play it or solve it i get stuck on lvl 31 out of sheer luck of getting there. but i also reread this post and noticed there is a lot of what you are talking about in the actual html on the page. maybe take a look at that? if you havent done it already. maybe in there somewhere for the game it may help. im on day 2 trying to solve lvl 31. with no luck =( and the program my friend designed gets me this far and has problems with it. here is a pic of the game im stuck on with the shapes to use and the program my friend made:
   maybe you all designed programs far beyond this one and if anyone could help or anything i would greatly appreciate it. i enjoy this game but its just inhumanly out of my brain power. lol |
|
|
|
|
#22 (permalink) |
|
Upright
|
I am working on solving Shapeshifter -- I'm up to level 41 at the moment -- and though this is an old thread, I imagine other solvers will find it just as I did, on Google, and may be interested in my progress toward a solution. My solver uses a combination of Python and 'C', and I'm considering a wholesale shift to APL. My program solved level 40 in an even 1000 seconds. It solved level 31 (which the previous poster was stuck on) in a little over 4 seconds.
I am very interested in how far the original poster got with their program. My page -> http://shewhoshapes.wordpress.com iLbi, my solver solved that board in 5.63 seconds. The (a) solution is: (0, 3) (2, 2) (3, 1) (1, 1) (3, 3) (2, 1) (1, 2) (0, 1) (0, 1) (1, 3) (1, 0) (0, 0) Last edited by Tipa; 07-13-2007 at 06:01 PM.. Reason: Automerged Doublepost |
|
|
|
|
#23 (permalink) |
|
Upright
Location: menlo park
|
i worked feverishly on this neopets game a couple years ago, writing a solver in Java that eventually shot towards the top. i eventually stopped running it when it became clear that the puzzle maxed out at 100: this was a big anticlimax. you can't really see who has the best solver, since a lot of people got to 100. and no doubt at all that it's all computer programs solving the puzzles. no human could get anywhere close.
i don't have most of the old levels, but here's what level 74 looked like:  i also had a python script to scrape the page, and another to submit the solution. there's a version of this puzzle at: http://www.hacker.org/modulo/ it's almost exactly the same, except here the difficulty ramps up without limit, the high scores are permanent, and computer program use is encouraged. people who have written solvers should try running them there -- the forum explains how it works. as for the algorithms i used -- well, it would be no fun to give away all the secrets  one thing for sure, it's a puzzle with serious depth. my final codebase was about 4000 lines of java. my ultimate solver combined a series of optimizations and pruning techniques, each shaving off an exponent from the solve time, just to have another exponent added by going a few levels higher. one thing for sure, it's a puzzle with serious depth. my final codebase was about 4000 lines of java. my ultimate solver combined a series of optimizations and pruning techniques, each shaving off an exponent from the solve time, just to have another exponent added by going a few levels higher.adum |
|
|
|
|
#24 (permalink) |
|
Upright
|
The solver program seen above can be found at
shapeshafter.neolanz.com It's a brute force random slammer. It's good to about level 31. level 1-15 solves in approximately 2 seconds level 16-20 solves in approximately 10 seconds level 21-25 solves in approximately 60 seconds level 26-29 solves in approximately 5 minute 30 in hours 32 in days 35 in weeks? |
|
|
|
|
#28 (permalink) |
|
Upright
|
...Um, ok, not sure what those last two posts were all about, but hi! I found this thread through google as I was racking my brains about how to solve this puzzle. I am at level 26 at the moment, and my solver from neolanz has taken about 20 minutes so far. It's still trying to solve as I'm typing this now (over 13 million tries). I'm rather disappointed by it, since in earlier posts I read that it should take about 5 minutes in my level range, making me wonder if the game has been changed at all from last year to now. Any ideas?
|
|
|
| Tags |
| shapeshifter, solve |
|
|